2 Sample Mean
Hypothesis t-test Example
Calculations by Professor S. Gramlich
Updated 3/22/09
9-3 #26 (from Triola,
“Elementary Statistics,” 10th ed, C2006, p. 482)
Blanking Out on Tests
Many students have had unpleasant experience of panicking on a test because the first
question was exceptionally difficult. The arrangement of test items was studied for its
effect on anxiety. The following scores are measures of “debilitating test anxiety,”
which most of us call panic or blanking out (base on data from “Item Arrangement,
Cogntive Entry Characterstics, Sex and Test Anxiety as Predictors of Achievement
in Examination Performance,” by Klimko, Journal of Experimental Education,
Vol. 52, No. 4). Is there sufficient evidence to support the claim that the
two populations of scores have the same mean? Is there sufficient evidence to support
the claim that the arrangement of the test items has an effect on the score?
Questions Arranged from Easy to Difficult Questions Arranged from Difficult to Easy
24.64 33.62
33.31 35.91
26.43 27.24
28.89 27.62
25.49 34.02
39.29 26.68
20.6 32.34
24.23 42.91
28.71 26.63
38.81 29.49
16.32 29.34
21.13 30.2
7.1 30.26
31.73 35.32
27.85 33.53
32.83 32.54
26.69
32.86
30.02
30.29
28.02
28.9
21.06
21.96
30.72
Step 1: Hypotheses
H0: μ1 = μ2 (original claim) or H0: μ1 - μ2 = 0
H1: μ1 ≠
μ2 H1: μ1 - μ2
≠ 0
(2 tailed test)
Step 2: Given
assume: alpha = 5% = .05; observations independent, normal, srs; σ1 & σ2 unknown
SAMPLE 1 stats (n1 = 25)
sample mean: xbar1 = Σx/n = (24.64+ 33.31+...+30.72)/ 25
or use excel "=AVERAGE(A2:A26)"
xbar1 = 27.115
sample standard deviation:
s1 = √[Σ(x-xbar)2 / (n-1)] = √[(24.64-27.115)2 + (33.31-27.115)2 +...+ (30.72-27.115)2] / (25-1)]
or use excel "=STDEV(A2:A26)"
s1 = 6.857
SAMPLE 2 stats (n2 = 16)
sample mean: xbar2 = Σx/n = (33.62 + 35.91 +...+ 32.54)/16
or use Excel "=AVERAGE(B2:B26)"
xbar2 = 31.728
sample standard deviation:
s2 = √[Σ(x-xbar)2 / (n-1)] = √[(33.62-31.728)2 + (35.91-31.728)2 +...+ (32.54-31.728)2/ (16-1)]
or use Excel "=STDEV(B2:B26)"
s2 = 4.26
Step 3: t critical value (cv)
use df smaller of df1 = n1-1 = 25-1 =24 or df2 = n2-1 = 16-1 =15 on Table A-3
so with df = 15 and tc= ±2.131 (2 tail)
or use Excel “=TINV(0.05,15)”
Step 4: t test statistic (ts)
t = [(xbar1 - xbar2) - (μ1 -
μ2)] / √[ s12/n1 + s22/n2]
= [(27.115 - 31.728) - 0] / √[6.8572/25 + 4.262/16]
= -4.613/ √[47.018/25 + 18.148/16]
= -4.613/ √[1.881 + 1.134]
= -4.613/ √[3.015]
= -4.613/ 1.736
t = -2.657
Step 5: Draw t curve, label cv, ts, & shade critical region
critical region in red divided into 2 tails
p-value in blue
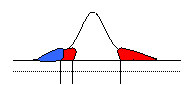
-2.657 -2.131 +2.131
Step 6: Traditional DR
Since t = -2.657 is inside critical region, Reject H0.
Step 7: P-Value
From Table A-3, with df = 15, t = -2.657 falls in between 2.947 & 2.602,
so 0.01 < P-val < 0.02
or use Excel “=TDIST(2.657,15,2)”
Step 8:
Since (0.01 < P-val < 0.02) < (α = .05), Reject H0.
Step 9: Confidence Interval (CI)
E = tc * √[ s12/n1 + s22/n2]
= 2.131 * 1.736 (from step 3 & 4)
= 3.699
μ1 - μ2 = (xbar1 - xbar2) ± E
= -4.613 ± 3.699
(xbar1 - xbar2) - E < μ1 - μ2 < (xbar1 - xbar2) + E
-4.613 - 3.699 < μ1 - μ2 < -4.613 +
3.699
-8.312 < μ1
- μ2 < -0.914
Step 10:
Since CI does not contain 0, Reject H0.
Step 11: Conclusion
There is not sufficient evidence to support the claim that the two populations have the same mean anxiety score. It appears that the arrangement of test items does have an effect on the score.