Correlation and Simple Regression Example

Calculations by Professor S. Gramlich

Updated 3/23/09

10-2 and 10-3 #14 (from Triola, “Elementary Statistics,” 10^th ed, C2006, pp. 535, 554)

Song Audiences and Sales

The table below lists the numbers of audience impressions (in hundreds of millions) listening to songs

and the corresponding numbers of albums sold (in hundreds of thousands). The number of audience

impressions is a count of the number of times people have heard the song. The table is based on

data from USA Today. Does it appear that album sales are affected very strongly by the number

of audience impressions? Find the best predicted number of albums sold for a song with

20 (hundred million) audience impressions.

Audiencee Impressionss	28	13	14	24	20	18	14	24	17
Albums Sold	19	7	7	20	6	4	5	25	12

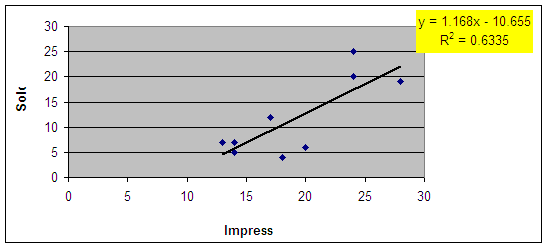
Scatterplot

Sample Stats

mean for x

xbar = Σx / n = (28 + 13 +...+ 24 + 17) / 9 = 19.1

standard deviation for x

s_x = √[Σ(x-xbar)² / (n-1)] = √[(28-19.1)² + (13-19.1)² +...+ (17-19.1)²] / (9-1)

= √[SS_x / (n-1)] = √[222.9/8] = 5.278

mean for y

ybar = Σy / n = (19 + 7 +...+ 12)/ 9 = 11.7

standard deviation for y

s_y = √[Σ(y-ybar)² / (n-1)] = √[(19-11.7)² + (7-11.7)² +...+ (11-11.7)²] / (9-1)

= √[SS_y / (n-1)] = √[480/8] = 7.746

covariance

s_xy = Σ(x-xbar)(y-ybar) / (n-1) = (28-19.1)(19-11.7) + (13-19.1)(7-11.7) +...+(17-19.1)(11-11.7)

= SS_xy / (n-1) = 260.3/8 = 32.542

Correlation

r = s_xy / (s_xs_y) = 32.542/(5.278*7.746) = .796

OR

= SS_xy / √[SS_xSS_y] = 260.3 / √[222.9*480] = .796

r Critical value

from Table A-6: n=9, α = 0.05, r_c = ±.666

Conclusion:

(critical region in red, p-value region in blue)

_________________________ Since r inside critical region, Reject H0.

| | | There appears to be a significant linear relationship

-.666 +.666 .796 between # of audience impressions and # of albums sold.

(also from Table A-6, .796 in between .666 and .798, so .05 > P-val > .01, Reject H0)

10-3 #14

Slope

b₁ = SS_xy / SS_x = 260.3 / 222.9 = 1.168

b₀ = ybar - b₁ * xbar = 11.7 - 1.168 * 19.1 = -10.655

Yhat = b₀ + b₁X = -10.655 + 1.168X

Yhat (20) = -10.655 + 1.168*20 = 12.7