MULTIPLE CHOICE. Choose the one
alternative that best completes the statement or answers the question.
Identify the given random variable as being discrete or continuous.
1) The braking time of a car.
A) Discrete B)
Continuous
Determine whether the following is a probability distribution. If not,
identify the requirement that is not satisfied.
2)

A) Not a probability distribution. B) Yes, a probability distribution.
Find the mean of the given probability distribution.
3) A police
department reports that the probabilities that 0, 1, 2, and 3 burglaries will
be reported in a given day are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ,
respectively.
,
respectively.
A) ![]() B)
B) ![]() C) 0.25 D) 1.50
C) 0.25 D) 1.50
Solve the problem.
4) In a certain
town, ![]() % of adults
have a college degree. The accompanying table describes the probability
distribution for the number of adults (among 4 randomly selected adults) who
have a college degree. Find the standard deviation for the probability
distribution.
% of adults
have a college degree. The accompanying table describes the probability
distribution for the number of adults (among 4 randomly selected adults) who
have a college degree. Find the standard deviation for the probability
distribution.
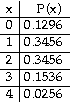
A) ![]() B)
B) ![]() C)
C) ![]() D)
D) ![]()
5) In a certain town, % of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults) who have a college degree. Find the variance for the probability distribution.
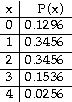
A)
B)
C)
D)
6) A 28-year-old man
pays $ for a one-year life insurance policy with coverage of . If the
probability that he will live through the year is , what is the expected value
for the insurance policy?
A)
B)
C)
D)
Determine whether the given procedure results in a binomial
distribution. If not, state the reason why.
7) Choosing 5 people
(without replacement) from a group of
people, of which 15 are women, keeping track of the number of men
chosen.
A) Not binomial: there are more than two outcomes for each
trial.
B) Procedure results in a binomial distribution.
C) Not binomial: there are too many trials.
D) Not binomial: the trials are not independent.
8) Spinning a
roulette wheel times, keeping track of
the occurrences of a winning number of "16".
A) Procedure results in a binomial distribution..
B) Not binomial: there are too many trials.
C) Not binomial: there are more than two outcomes for each
trial.
D) Not binomial: the trials are not independent.
Find the indicated probability.
9) Suppose that in a certain
town, percent of the voters favor a new
ballpark. Find the probability that among voters questioned, exactly of them favor the new ballpark.
A)
B)
C)
D)
10) A company
purchases shipments of machine components and uses this acceptance sampling
plan: Randomly select and test ![]() components and accept the whole batch if there
are fewer than 3 defectives. If a particular shipment of thousands of
components actually has a
components and accept the whole batch if there
are fewer than 3 defectives. If a particular shipment of thousands of
components actually has a ![]() % rate of
defects, what is the probability that this whole shipment will be accepted?
% rate of
defects, what is the probability that this whole shipment will be accepted?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
11) An airline
estimates that % of people booked on their flights actually show up. If the
airline books people on a flight for
which the maximum number is , what is the probability that the number of people
who show up will exceed the capacity of the plane?
A)
B)
C)
D)
12) A car insurance
company has determined that % of all drivers were involved in a car accident
last year. Among the drivers living on
one particular street, 3 were involved in a car accident last year. If drivers are randomly selected, what is the
probability of getting 3 or more who were involved in a car accident last year?
A)
B)
C)
D)
13) In a study, ![]() % of adults
questioned reported that their health was excellent. A researcher wishes to
study the health of people living close to a nuclear power plant. Among
% of adults
questioned reported that their health was excellent. A researcher wishes to
study the health of people living close to a nuclear power plant. Among ![]() adults randomly selected from this area, only
3 reported that their health was excellent. Find the probability that when
adults randomly selected from this area, only
3 reported that their health was excellent. Find the probability that when ![]() adults are randomly selected, 3 or fewer are
in excellent health.
adults are randomly selected, 3 or fewer are
in excellent health.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Use the given values of n and p to find the minimum usual value m - 2s and the maximum usual
value m + 2s.
14) n = ![]() , p =
, p = ![]()
A) Minimum: ![]() ;
maximum:
;
maximum: ![]()
B) Minimum: ![]() ; maximum:
; maximum: ![]()
C) Minimum: ![]() ;
maximum:
;
maximum: ![]()
D) Minimum: ![]() ; maximum:
; maximum: ![]()
Solve the problem.
15) A die is rolled ![]() times and the number of times that two shows
on the upper face is counted. If this experiment is repeated many times, find
the mean for the number of twos.
times and the number of times that two shows
on the upper face is counted. If this experiment is repeated many times, find
the mean for the number of twos.
A) ![]()
B) 1.15
C) 1.05
D) 1.11
16) A die is rolled ![]() times and the number of twos that come up is
tallied. If this experiment is repeated many times, find the standard deviation
for the number of twos.
times and the number of twos that come up is
tallied. If this experiment is repeated many times, find the standard deviation
for the number of twos.
A) 1.33
B) 1.15
C) 1.05
D) 1.11
Determine if the outcome is unusual. Consider as unusual any result that
differs from the mean by more than 2 standard deviations. That is, unusual
values are either less than m - 2s or greater than m + 2s.
17) According to
AccuData Media Research, 36% of televisions within the Chicago city limits are
tuned to "Eyewitness News" at 5:00 pm on Sunday nights. At 5:00 pm on
a given Sunday, 2500 such televisions are randomly selected and checked to
determine what is being watched. Would it be unusual to find that ![]() of the 2500 televisions are tuned to
"Eyewitness News"?
of the 2500 televisions are tuned to
"Eyewitness News"?
A) Yes
B) No
Use the Poisson Distribution to find the indicated probability.
18) The number of
lightning strikes in a year at the top of a particular mountain has a Poisson
distribution with a mean of ![]() . Find the
probability that in a randomly selected year, the number of lightning strikes
is
. Find the
probability that in a randomly selected year, the number of lightning strikes
is ![]() .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
19) For a certain
type of fabric, the average number of defects in each square foot of fabric is ![]() . Find the
probability that a randomly selected square foot of the fabric will contain
more than one defect.
. Find the
probability that a randomly selected square foot of the fabric will contain
more than one defect.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
MULTIPLE CHOICE. Choose the one
alternative that best completes the statement or answers the question.
1) B
ID: STAT8T
4.2.1-7
Page Ref:
181-182
Objective:
(4.2) Classify Random Variable as Discrete or Continuous
2) A
ID: STAT8T
4.2.2-3+
Page Ref:
183-184
Objective:
(4.2) *Determine Whether Probability Distribution is Described
3) B
ID: STAT8T
4.2.3-7
Page Ref:
184-185
Objective:
(4.2) Find Mean for Probability Distribution
4) C
ID: STAT8T
4.2.4-5
Page Ref:
184-185
Objective:
(4.2) Find Standard Deviation/Variance for Probability Distribution
5) A
ID: STAT8T
4.2.4-6
Page Ref:
184-185
Objective:
(4.2) Find Standard Deviation/Variance for Probability Distribution
6) B
ID: STAT8T
4.2.5-5
Page Ref:
188-190
Objective:
(4.2) Find Expected Value
7) D
ID: STAT8T
4.3.1-5
Page Ref:
194-196
Objective:
(4.3) Det if Procedure Results in Binomial Distribution
8) A
ID: STAT8T
4.3.1-10
Page Ref:
194-196
Objective:
(4.3) Det if Procedure Results in Binomial Distribution
9) A
ID: STAT8T
4.3.2-4
Page Ref:
196-199
Objective:
(4.3) Solve Apps: Find Probability of Exactly x Successes
10) B
ID: STAT8T
4.3.3-5
Page Ref:
198-199
Objective:
(4.3) Solve Apps: Find Probability of at Least/at Most x Successes
11) C
ID: STAT8T
4.3.3-6
Page Ref:
198-199
Objective:
(4.3) Solve Apps: Find Probability of at Least/at Most x Successes
12) A
ID: STAT8T
4.3.3-9
Page Ref:
198-199
Objective:
(4.3) Solve Apps: Find Probability of at Least/at Most x Successes
13) A
ID: STAT8T
4.3.3-7
Page Ref:
198-199
Objective:
(4.3) Solve Apps: Find Probability of at Least/at Most x Successes
14) A
ID: STAT8T
4.4.3-6
Page Ref:
207
Objective:
(4.4) Find Min/Max Usual Value for Binomial Distrib
15) A
ID: STAT8T
4.4.4-2+
Page Ref:
205-206
Objective:
(4.4) Solve Apps: Means for Binomial Distribution
16) C
ID: STAT8T
4.4.5-2+
Page Ref:
205-206
Objective:
(4.4) Solve Apps: SD/Variances for Binomial Distribution
17) A
ID: STAT8T
4.4.6-6+
Page Ref:
207
Objective:
(4.4) Determine if Outcome is Unusual (Y/N)
18) C
ID: STAT8T
4.5.1-6
Page Ref:
211-213
Objective:
(4.5) Use Mean of Poisson Distrib to Find Probability
19) B
ID: STAT9T
4.5.1-7
Page Ref:
212-215
Objective:
(4.5) Use Mean of Poisson Distribution to Find Probability