MULTIPLE CHOICE.
Choose the one alternative that best completes the statement or answers
the question.
Perform the matrix operation, if possible.
1) Let A = ![]() . Find
. Find ![]() A.
A.
A)
![]()
B)
![]()
C)
![]()
D)
![]()
2) Let A =![]() and B
=
and B
= ![]() . Find
. Find ![]() A + B.
A + B.
A)
![]()
B)
![]()
C)
![]()
D)
![]()
3) Let A = ![]() and B =
and B = ![]() . Find
A + B.
. Find
A + B.
A)
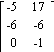
B)
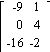
C)
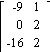
D)
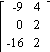
4) Let A = ![]() and B =
and B = ![]() . Find
A - B.
. Find
A - B.
A)
![]()
B)
![]()
C)
![]()
D)
![]()
Solve the problem.
5) The matrix shows
the average number of wax and buff treatments each of 3 workers in a car wash
can do in a day. Give the matrix that shows what each worker can do in ![]() days.
days.
Wax
Buffs
![]()
![]()
![]()
A)
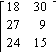
B)
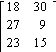
C)
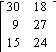
D)
![]()
Find the transpose of the matrix.
6)
![]()
A)
![]()
B)
![]()
C)
![]()
D)
![]()
Write the linear system as a matrix equation of the form
AX = B.
7) x +
y + z = ![]()
![]() x
x ![]() y
y ![]() z =
z = ![]()
![]() x
x ![]() y
y ![]() z =
z = ![]()
A)
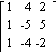
![]() =
= ![]()
B)
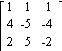
![]() =
=![]()
C)
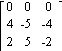
![]() =
=![]()
Write the matrix equation as a system of linear
equations.
8)
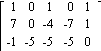
![]() =
= ![]()
A) x + y + z = ![]()
7x ![]() y
y ![]() z
+ w
=
z
+ w
= ![]()
-x ![]() y
y ![]() z
z ![]() w =
w = ![]()
B) x + z
+ v = ![]()
7x ![]() z
z ![]() w
+ v =
w
+ v = ![]()
-x ![]() y
y ![]() z
z ![]() w =
w = ![]()
C) x + 7y - z
= ![]()
![]() z =
z = ![]()
x ![]() y
y ![]() z =
z = ![]()
![]() y
y ![]() z =
z = ![]()
x + y = ![]()
Find the
indicated matrix, if possible.
9) A = ![]() , B =
, B =
![]() Find AB.
Find AB.
A)
![]()
B) AB is not defined.
C)
![]()
D)
![]()
10) A = ![]() , B
=
, B
= ![]() . Find BA.
. Find BA.
A)
![]()
B) AB is not defined.
C)
![]()
D)
![]()
11) A = ![]() , B =
, B =
![]() Find AB - I.
Find AB - I.
A)
![]()
B)
![]()
C)
![]()
D)
![]()
12) A = ![]() , B =
, B = ![]() . Find
. Find ![]() + 2B
+ 2B
A)
![]()
B)
![]()
C)
![]()
D)
![]()
TRUE/FALSE.
Write 'T' if the statement is true and 'F' if the statement is false.
13) AB = BA
14) (c + K)A = cA + KA
for any real numbers c and K
MULTIPLE CHOICE.
Choose the one alternative that best completes the statement or answers
the question.
Solve the problem.
15) The following table shows the market prices per pound that a trucker can get for his load of fruit in three cities: San Francisco (S.F.), Las Vegas (L.V.), and Los Angeles (L.A)
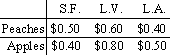
The trucker has a load of ![]() pounds of peaches and 3000 pounds of
apples. Write the information from the
table as a 2 x 3 matrix B. Write a row matrix A for which the entries represent
the number of pounds of each type of fruit in the truck. If C = AB, find c13.
What does this entry of C represent?
pounds of peaches and 3000 pounds of
apples. Write the information from the
table as a 2 x 3 matrix B. Write a row matrix A for which the entries represent
the number of pounds of each type of fruit in the truck. If C = AB, find c13.
What does this entry of C represent?
A) c13 = ![]() . c13
represents the total value of the peaches .
. c13
represents the total value of the peaches .
B) c13 = ![]() . c13
represents the total value of the apples.
. c13
represents the total value of the apples.
C) c13 = ![]() . c13
represents the total value of the load in Los Angeles.
. c13
represents the total value of the load in Los Angeles.
D) c13 = ![]() . c13
represents the total value of the load in Las Vegas.
. c13
represents the total value of the load in Las Vegas.
Determine whether the two matrices are inverses of each
other by computing their product.
16) ![]() ,
, 
A) Yes
B) No
Use the given inverse of the coefficient matrix to solve
the system of equations.
17) 5x \'2B ![]() y \'3D
y \'3D ![]() ,
,
2x \'2B ![]() y \'3D
y \'3D ![]() ;
;
The inverse of the coefficient matrix A = ![]() is
is ![]() =
= ![]() .
.
A) (![]() ,
, ![]() )
)
B) (![]() ,
, ![]() )
)
C) (![]() ,
, ![]() )
)
D) (![]() ,
, ![]() )
)
Find the inverse, if it exists, of the given matrix.
18) A = ![]()
A)
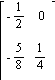
B) No inverse
C)
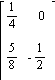
D)
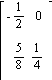
19) A = 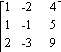
A) Does not exist
B)
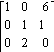
C)
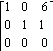
D)
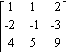
Solve the system by using the inverse of the coefficient
matrix.
20) x - y ![]() z =
z = ![]()
![]() x +
z =
x +
z = ![]()
x ![]() y
+ z =
y
+ z = ![]()
A) No solution
B) (![]() ,
, ![]() ,
, ![]() )
)
C) (![]() ,
, ![]() ,
, ![]() )
)
D) (![]() ,
, ![]() ,
, ![]() )
)
Solve the problem by setting up a system of equations,
rewriting the system as a matrix equation, and using the inverse of the
coefficient matrix to solve the system.
21) A printing
service is planning to purchase some new copy machines to meet its consumer
needs. It is considering a Model A machine which costs $3000 and prints at the
rate of 35 pages per minute, a Model B machine which costs $5000 and prints at
a rate of 50 pages per minute, and a Model C machine which costs $7000 and
prints at the rate of 60 pages per minute. The company has budgeted a total of
$94,000 for the purchase of the machines and wants to be able to print a total
of 57,600 pages per hour. For these models, it wants to purchase twice as many
Model A machines as Model B machines. Assuming that the budget and printing
needs are exactly met, how many of each model should be purchased?
A) 14 of Model A, 7 of Model B, 2 of Model C
B) 10 of Model A, 5 of Model B, 5 of Model C
C) 12 of Model A, 6 of Model B, 4 of Model C
D) 8 of Model A, 4 of Model B, 7 of Model C
Find the inverse of the diagonal matrix.
22)
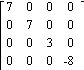
A)

B)

C)
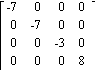
D)

Use matrix algebra with the given data to find the least
squares regression line. Round the
final values to three significant digits, if necessary.
23) In the table below, x represents the number of years since 2000 and y represents the population (in thousands) of the town Boomville. Find the least squares regression line which can be used to predict the population of Boomville (in thousands) in any given year.
![]()
A) y = 25x - 5
B) y = 12x + 20
C) y = 18x + 8
D) y = 28x - 10
MULTIPLE CHOICE.
Choose the one alternative that best completes the statement or answers
the question.
1) A
ID: FM3Yc1-5
3.1.2-1
Page Ref:
Objective:
Add/Subtract/Scalar Multiply Matrices
2) D
ID: FM3Yc1-5
3.1.2-4
Page Ref:
Objective:
Add/Subtract/Scalar Multiply Matrices
3) C
ID: FM3Yc1-5
3.1.2-7
Page Ref:
Objective:
Add/Subtract/Scalar Multiply Matrices
4) D
ID: FM3Yc1-5
3.1.2-8
Page Ref:
Objective:
Add/Subtract/Scalar Multiply Matrices
5) A
ID: FM3Yc1-5
3.1.5-10
Page Ref:
Objective:
Solve Apps: Add/Subtract/Scalar Multiply Matrices
6) D
ID: FM3Yc1-5
3.1.6-3
Page Ref:
Objective:
Find Transpose of Matrix
7) B
ID: FM3Yc1-5
3.2.1-2
Page Ref:
Objective:
Write Linear System as Matrix Equation
8) B
ID: FM3Yc1-5
3.2.2-3
Page Ref:
Objective:
Write Matrix Equation as Linear System
9) A
ID: FM3Yc1-5
3.2.3-2
Page Ref:
Objective:
Find Matrix Product
10) B
ID: FM3Yc1-5
3.2.3-3
Page Ref:
Objective:
Find Matrix Product
11) A
ID: FM3Yc1-5
3.2.3-7
Page Ref:
Objective:
Find Matrix Product
12) A
ID: FM3Yc1-5
3.2.3-10
Page Ref:
Objective:
Find Matrix Product
TRUE/FALSE.
Write 'T' if the statement is true and 'F' if the statement is false.
13) FALSE
ID: FM3Yc1-5
3.2.4-2+
Page Ref:
Objective:
Determine Truth of Matrix Statement (T/F)
14) TRUE
ID: FM3Y
3.2.4-7+
Page Ref:
126-135
Objective:
(3.2) Determine Truth of Matrix Statement (T/F)
MULTIPLE CHOICE.
Choose the one alternative that best completes the statement or answers
the question.
15) C
ID: FM3Yc1-5
3.2.6-5
Page Ref:
Objective:
Solve Apps: Matrix Products (Miscellaneous)
16) A
ID: FM3Y
3.3.1-5
Page Ref:
138-142
Objective:
(3.3) Determine Whether Matrices are Inverses
17) B
ID: FM3Y
3.3.2-1
Page Ref:
138-142
Objective:
(3.3) Solve System of Eqns Given Inverse of Coefficient Matrix
18) D
ID: FM3Y
3.3.3-4
Page Ref:
143-144
Objective:
(3.3) Find Inverse of 2 x 2 Matrix
19) A
ID: FM3Y
3.3.4-2
Page Ref:
143-144
Objective:
(3.3) Find Inverse of 3 x 3 Matrix
20) B
ID: FM3Y
3.3.7-5
Page Ref:
144-146
Objective:
(3.3) Solve System of Equations Using Matrix Inverse
21) C
ID: FM3Y
3.3.8-10
Page Ref:
144-146
Objective:
(3.3) Solve Apps: Solve System Using Matrix Inverse
22) B
ID: FM3Y
3.3.9-3
Page Ref:
138-146
Objective:
(3.3) Find Inverse of Diagonal Matrix
23) A
ID: FM3Y
1.5.6-6+
Page Ref:
51-60
Objective:
(1.5) Solve Apps: Find Regression Equation