MULTIPLE CHOICE. Choose the one
alternative that best completes the statement or answers the question.
Write the requested matrix for the system of equations.
1) w + ![]() x + y
x + y ![]() z =
z = ![]() Write the augmented matrix.
Write the augmented matrix.
2w - x
![]() z =
z = ![]()
-w - 2x ![]() y =
y = ![]()
A) 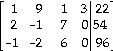 B)
B) 
C) 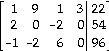 D)
D) 
Write the system of equations associated with the augmented matrix. Do
not solve.
2)
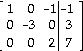
A) x - z =![]()
-3y =![]()
2z =![]() B) x - z =
B) x - z =![]()
-3z
=![]()
2z =![]()
C) x =![]()
-3y =![]()
-x + 2z =![]() D) x - y
=
D) x - y
=![]()
-3y =![]()
2z =![]()
Find the system of equations that models the problem. Do not solve.
3) A department of a factory hires semiskilled workers, skilled
workers, and managers. Each semi skilled
worker is paid $10 per hour, each skilled worker is paid $![]() per
hour, and each manager is paid $25 per
hour. The department is allowed an
hourly payroll of $2930 for these three types of workers. Each worker must
spend some time in training each week: semiskilled workers 4 hours , skilled workers
5 hours, and managers 2 hours. The training center can handle a maximum of 1050
person-hours each week. The department needs 230 skilled and semiskilled
workers to meet production schedules. Assumung that the allowable payroll is
met, the training center is fully utilized, and production needs are met, how
many of each type of worker does the department need?
per
hour, and each manager is paid $25 per
hour. The department is allowed an
hourly payroll of $2930 for these three types of workers. Each worker must
spend some time in training each week: semiskilled workers 4 hours , skilled workers
5 hours, and managers 2 hours. The training center can handle a maximum of 1050
person-hours each week. The department needs 230 skilled and semiskilled
workers to meet production schedules. Assumung that the allowable payroll is
met, the training center is fully utilized, and production needs are met, how
many of each type of worker does the department need?
Let
x represent the number of semiskilled workers, y the number of skilled workers,
and z the number of managers.
A) 10x + 4y = 2930
![]() x + 5y = 1050
x + 5y = 1050
25y + 2z = 230 B) 10x + 25y + 13z = 2930
4x + 5y + 2z = 1050
x + y = 230
C) 10x + ![]() y + 25z =
2930
y + 25z =
2930
4x + 5y + 2z = 1050
x + y = 230
D) 10x + ![]() y + 25z =
2930
y + 25z =
2930
4x + 5y = 1050
x + y + z = 230
Perform the row operations on the matrix and write the resulting matrix.
4) Replace ![]() by
by ![]()
![]() +
+ ![]()
![]()
![]()
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]()
5) Replace ![]() by
by ![]()
![]()
![]()
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]()
Use the pivoting process to put the augmented matrix into reduced row-echelon
form.
6) 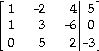
A) 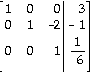 B)
B) 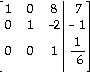
C) 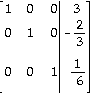 D)
D) 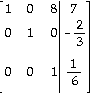
Solve the system.
7) ![]() x + y =
x + y =![]()
![]() x
x ![]() y =
y =![]()
A) (![]() ,
, ![]() ) B) No solution C) (
) B) No solution C) (![]() ,
, ![]() ) D) (
) D) (![]() ,
, ![]() )
)
Use the Gauss-Jordan method to solve the system of equations.
8) 2x - 2y + 3z = ![]()
x + 2y - z = ![]()
2y + z = ![]()
A) (![]() ,
, ![]() ,
, ![]() ) B) (
) B) (![]() ,
, ![]() ,
, ![]() ) C) No
solution D) (
) C) No
solution D) (![]() ,
, ![]() ,
, ![]() )
)
9) x - y + 8z = -107
x + 2y = 21
2x
+ y + 8z = -80
A) (5, 8, -13) B) (5, 8, 0) C) No solution D) (5, 8, 7)
Solve the problem by writing and solving a suitable system of equations.
10) Julia is preparing a meal by combining three ingredients. One unit of each ingredient provides the following quantities (in grams) of carbohydrates, fat, and protein.
Protein(g) Carbohydrates(g) Fat (g)
Ingredient A 3 3 1
Ingredient B 2 4 2
Ingredient C 4 5 1
Ideally the meal should contain ![]() of protein,
of protein, ![]() of carbohydrates, and
of carbohydrates, and ![]() of fat. How many units of each ingredient
should Julia use?
of fat. How many units of each ingredient
should Julia use?
A) ![]() grams of ingredient A,
grams of ingredient A,
![]() grams of ingredient B,
grams of ingredient B, ![]() grams of ingredient C
grams of ingredient C
B) ![]() grams of ingredient
A,
grams of ingredient
A, ![]() grams of ingredient B,
grams of ingredient B, ![]() grams of ingredient C
grams of ingredient C
C) ![]() grams of ingredient
A,
grams of ingredient
A, ![]() grams of ingredient B,
grams of ingredient B, ![]() grams of ingredient C
grams of ingredient C
D) ![]() grams of ingredient
A,
grams of ingredient
A, ![]() grams of ingredient B,
grams of ingredient B, ![]() grams of ingredient C
grams of ingredient C
Find the solutions, if any exist. Write the solutions in parametric
form.
11) x - y - 5z = ![]()
y + 3z = ![]()
x + y + z = ![]()
A) (0, 0, ![]() )
)
B) x = 2z + ![]() , y = -3z
+
, y = -3z
+ ![]() , z = any
real number
, z = any
real number
C) x = 3z + ![]() , y = -3z
+
, y = -3z
+ ![]() , z = any
real number
, z = any
real number
D) x = 2z - ![]() , y = -3z
-
, y = -3z
- ![]() , z = any
real number
, z = any
real number
12) y + ![]() z =
z = ![]()
-x + ![]() z =
z = ![]()
x + y
= ![]()
A) x = ![]() z -
z - ![]() , y =
, y = ![]() -
- ![]() z, z =
any real number
z, z =
any real number
B) x = ![]() , y =
, y = ![]() , z = 0
, z = 0
C) x = ![]() z -
z - ![]() , y =
, y = ![]() +
+ ![]() z, z =
any real number
z, z =
any real number
D) x = ![]() z +
z + ![]() , y =
, y = ![]() -
- ![]() z, z =
any real number
z, z =
any real number
13) x + y +
z
= 9
2x
- 3y + 4z = 7
A) x = ![]() , y =
, y = ![]() , z = any
number
, z = any
number
B) x = ![]() , y =
, y = ![]() , z = any
number
, z = any
number
C) x = ![]() , y =
, y = ![]() , z = any
number
, z = any
number
D) x = ![]() , y =
, y = ![]() , z = any
number
, z = any
number
Solve the problem by writing and solving a suitable system. Write the
solution in parametric form.
14) A school library has $![]() to spend
on new books among the four categories of biology, chemistry, physics, and
mathematics. If the amount spent on biology books is to be the same as the
amount spent on chemistry books and if the amount spent on mathematics books is
to be the same as the total spent on chemistry and physics books, how can the
money be distributed among the four types of books? (Let x denote the amount
spent on biology books, y the amount spent on chemistry books, z the amount
spent on physics books, and w the amount spent on mathematics books.)
to spend
on new books among the four categories of biology, chemistry, physics, and
mathematics. If the amount spent on biology books is to be the same as the
amount spent on chemistry books and if the amount spent on mathematics books is
to be the same as the total spent on chemistry and physics books, how can the
money be distributed among the four types of books? (Let x denote the amount
spent on biology books, y the amount spent on chemistry books, z the amount
spent on physics books, and w the amount spent on mathematics books.)
A) x = $![]() - w, y =
$
- w, y =
$![]() - w, z =
2w - $
- w, z =
2w - $![]() ,
, ![]()
B) x = $![]() + w, y =
$
+ w, y =
$![]() + w, z =
w - $
+ w, z =
w - $![]() ,
, ![]()
C) x = $![]() - 2w, y
= $
- 2w, y
= $![]() - 2w, z
= 3w - $
- 2w, z
= 3w - $![]() ,
, ![]()
D) x = $![]() - 3w, y
= $
- 3w, y
= $![]() - 3w, z
= 4w - $
- 3w, z
= 4w - $![]() ,
, ![]()
MULTIPLE CHOICE. Choose the one
alternative that best completes the statement or answers the question.
1) D
ID: FM3Yc1-5
2.1.1-9
Objective: Write
Augmented/Coefficient Matrix Given System
2) A
ID: FM3Yc1-5
2.1.2-4
Objective:
Write System of Equations Given Augmented Matrix
3) C
ID: FM3Yc1-5
2.1.3-6
Objective:
Solve Apps: Find System of Eqns to Model Problem (Miscellaneous)
4) B
ID: FM3Yc1-5
2.2.1-4
Objective:
Perform Row Operations on Augmented Matrix
5) C
ID: FM3Yc1-5
2.2.1-5
Objective:
Perform Row Operations on Augmented Matrix
6) C
ID: FM3Yc1-5
2.2.2-3+
Objective:
Transform Augmented
Matrix to Reduced Row-Echelon Form
7) C
ID: FM3Yc1-5
2.2.3-1
Objective:
Solve System in
Two Variables by Gauss Jordan
8) A
ID: FM3Yc1-5
2.2.4-8
Objective:
Solve System in Three Variables by Gauss Jordan (One Solution)
9) C
ID: FM3Yc1-5
2.2.5-6
Objective:
Solve System in Three Variables by Gauss Jordan (No Solution)
10) A
ID: FM3Yc1-5
2.2.7-6
Objective:
Solve Apps: Solve System of Equations I
11) B
ID: FM3Yc1-5
2.3.1-1
Objective:
Solve Dependent System in Three Variables I
12) A
ID: FM3Yc1-5
2.3.2-3
Objective:
Solve Dependent System in Three Variables II
13) A
ID: FM3Yc1-5
2.3.2-4
Objective:
Solve Dependent System in Three Variables II
14) C
ID: FM3Yc1-5
2.3.7-5
Objective:
Solve Apps: Linear Systems with Many Solutions