Professor Gramlich
Due Date: April 29, 2010 Math 017 Elementary Algebra
TAKE HOME
EXAM 3
Pleas follow “Directions for Handing in Assignments” under “Class Materials” on my website.
Make sure you have the proper heading, show all your work neatly, staple your pages, and circle answers.
All questions are from the “Elementary Algebra” customized green text by Bittinger.
#1 (3.5) page 246, #30 (23 points total)
2x + y
= 13
4x + 2y = 23
Do by the following methods:
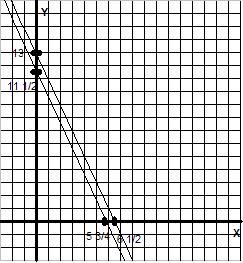
1) Graphical (also, state intercepts, conclusion, and slopes). (13 points, +1 bonus for exact slope)
2x + y =13
x-intercept y-intercept
2x + 0 = 13 2(0) + y =13
2x = 13 0 + y =13
2x/2 = 13/2 y = 13
x = 13/2 = 6 ½ (0, 13)
(6 ½, 0)
slope (solve literally for y): -2x + 2x + y = 13 – 2x
0 + y = 13 – 2x
y = 13 – 2x
y = mX + b => y = -2x + 13
where m = slope = -2 (falling)
4x + 2y = 23
x-intercept y-intercept
4x + 2(0) =23 4(0) + 2y =23
4x = 23 2y = 23
4x/4 = 23/4 2y/2 = 23/2
x = 23/ 4 = 5 ¾ y = 23/2 = 11 ½
(5 ¾, 0) (0, 11 ½)
slope (solve literally for y): -4x + 4x + 2y = 23 – 4x
2y = 23 – 4x
2y/2 = 23/2 – 4x/2
y = 23/2 – 2x
y = mX + b => y = -2x + 23/2
where
m = slope = -2
(falling)
2x + y = 13
4x + 2y =23
lines parallel so No Solution, Inconsistent Set
2) Substitution (5 points)
solve literally for y in top equation 2x + y =13
-2x + 2x + y = 13 – 2x
y = 13 – 2x
substitute for y in bottom equation 4x + 2y = 23
4x + 2(13 – 2x) = 23
distribute: 4x + 26 – 4x = 23
26 ≠ 23
No Solution, Inconsistent Set
3) Addition (5 points)
multiply top equation by –2: -2(2x + y = 13)
add: -4x – 2y = -26
+
(4x + 2y = 23)
0 + 0 = -3
0 ≠ -3
No Solution, Inconsistent Set
#2 (3.5) page 245, #12 (22 points total)
2x + 3y = 4
-2x – 3y = -4
Do by the following methods:
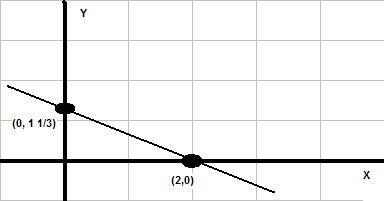
1) Graphical (also, state intercepts, conclusion, and slopes). (13 points, +1 bonus for exact slope)
2x + 3y = 4
x-intercept y-intercept
2x + 0 = 4 0 + 3y = 4
2x = 4 3y = 4
2x/2 = 4/2 3y/3 = 4/3
x = 2 y = 4/3 = 1 1/3
(2,0) (0, 1 1/3)
slope (solve literally for y): -2x + 2x + 3y = 4 – 2x
3y/3 = 4/3 – 2x/3
y = 4/3 – 2x/3
y = mX + b => y = -2x/3 + 4/3
where m = slope = -2/3 (falling)
-2x – 3y = -4
x-intercept y-intercept
-2x + 0 = -4 0 – 3y = -4
-2x = -4 -3y = -4
-2x/-2 = -4/-2 -3y/-3 = -4/-3
x = +2 y = +4/3 = +1 1/3
(2,0) (0, 1 1/3)
slope (solve literally for y): +2x – 2x – 3y = -4 + 2x
0 – 3y = -4 + 2x
-3y/(-3) = -4/(-3) + 2x/ (-3)
y = +4/3 – 2x/3
y = mX + b => y = -2x/3 + 4/3
where m = slope = -2/3 (falling)
Same line so Infinitely Many Solution (all Real #’s), Dependent Set
2) Substitution (5 points)
solve literally for y in top equation 2x + 3y = 4
-2x + 2x + 3y = 4 – 2x
3y = 4 – 2x
y = 4/3 – 2x/3
substitute for y in bottom equation -2x – 3y = -4
-2x – 3(4/3 – 2x/3) = -4
distribute –2x – 4 + 2x = -4
-4 = -4
Infinitely Many Solution (all Real #’s), Dependent Set
3) Addition (4 points)
2x + 3y = 4
+ (-2x
– 3y = -4)
0 + 0 = 0
Infinitely Many Solution (all Real #’s), Dependent Set
#3 (3.6) page 257, #20 (10 points total)
Also, define variables, show equations, and final answer units.
Clear Shine window cleaner is 12% alcohol and Sunstream window cleaner is 30% alcohol.
How much of each should be used to make 90 oz of a cleaner that is 20% alchol.
Variables (2 points)
Let C = oz. of Clear Shine
window cleaner
S = oz. of Sunstream window cleaner
Equations (2 points)
(total) C + S = 90 oz
(alcohol) .12C + .30S = .20(90)
using Addition method & multiplying top equation by -.12
-.12C - .12S = -.12(90) => .12C - .12S = -10.8
.12C + .30S = .20(90) => + (.12C + .3S = 18)
.18S = 7.2
S = 40 oz.
C + 40 = 90
C = 50 oz.
Check
C + S = 90 => 50 + 40 =90
.12C + .3S = .2(90) => .12(50) + .3(40) = 18
6 + 12 = 18